Nested Learning: The Illusion of Deep Learning Architecture

https://abehrouz.github.io/files/NL.pdf

TL;DR

作者认为所谓的“深度学习架构”和“优化器”本质上是一回事，它们都是嵌套的优化问题。基于此，论文提出了嵌套学习（Nested Learning, NL） 范式，并设计了Hope架构（包含自我修正模块和连续记忆系统），旨在让模型像人脑一样拥有多时间尺度的记忆和持续学习能力，从而打破“预训练”和“推理”的界限。

INFO

这篇论文并没有开源，其中使用的 Titans 模型论文也没有开源，且这两篇文章的作者是同一个人，请批判性接受下面的内容

文章有一些数学推导，我没有补充到下面的讲解中

1. 核心 Insight 与神经科学动机

1.1 核心批判：深度学习的“错觉”与“失忆”

架构的错觉： 传统观点将“模型架构”（如 Transformer）和“优化器”（如 Adam）视为两个独立的东西。作者认为这是一个错觉。在 NL 视角下，优化器本身就是一个记忆模块，它试图通过压缩梯度来学习；而架构本身就是一个优化过程。
顺行性遗忘症（Anterograde Amnesia）类比： 当前的 LLM（大语言模型）像患有顺行性遗忘症的病人。一旦预训练结束（发病），模型就无法将新发生的上下文（短期记忆）转化为长期记忆（权重更新）。模型只能在有限的上下文窗口内“体验当下”，而无法真正地持续学习。

1.2 神经科学启发：多时间尺度处理

脑波频率： 人脑通过不同频率的脑波（Gamma 波处理感官信息，Theta/Delta 波处理记忆巩固）来协调计算。
统一且可重用的结构： 大脑皮层结构是统一的（例如切除半个大脑，剩下的部分可以重组功能）。
NL 的哲学： 模型不应由异构的层组成，而应由统一的MLP（多层感知机） 块组成，区别仅在于它们的更新频率（Update Frequency）。

2. 理论框架：嵌套学习 (Nested Learning)

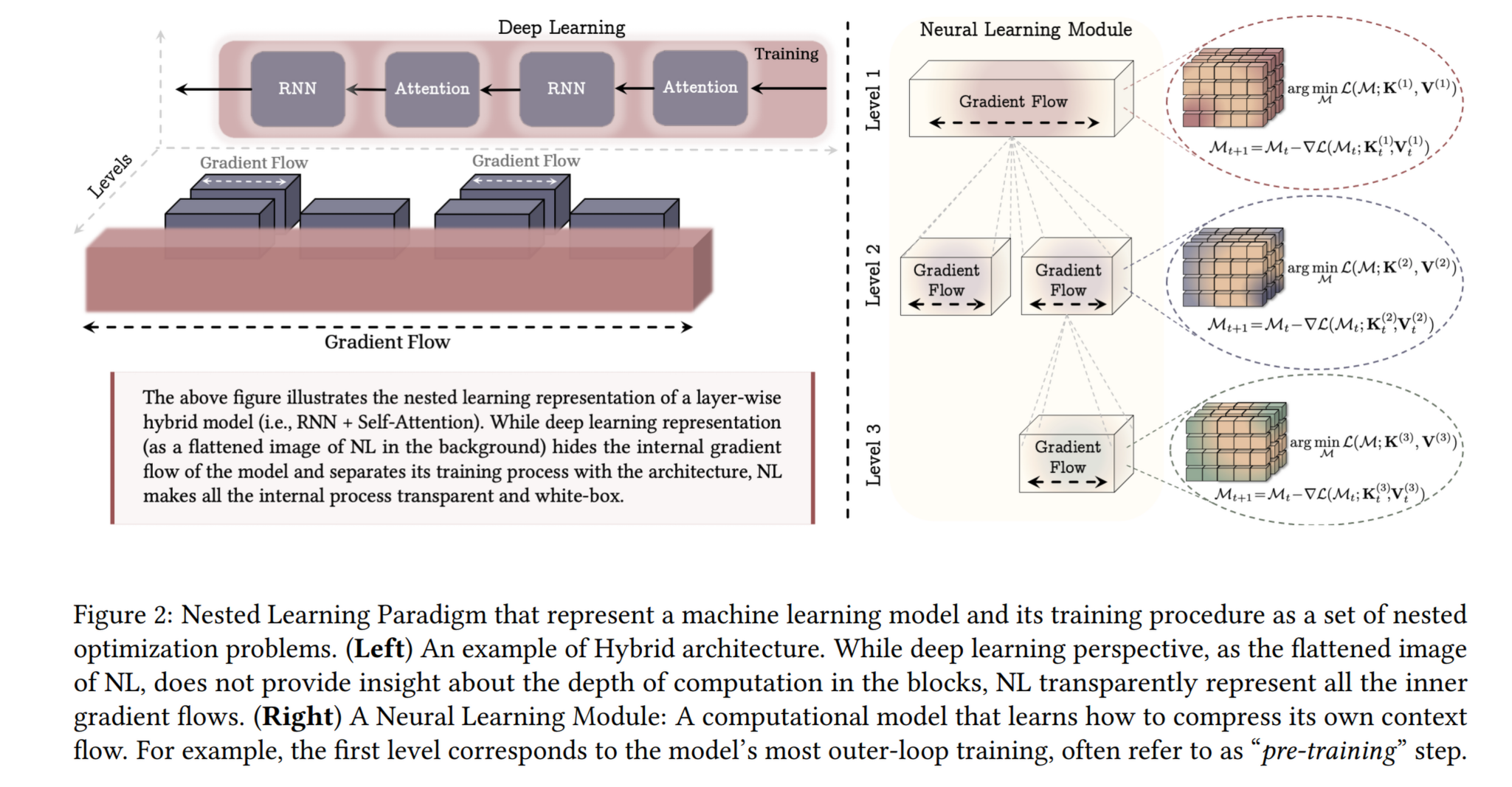
这是论文的理论基石。作者提出，任何机器学习系统都可以被分解为一组嵌套的、多层级的优化问题。

We argue that the optimization process and the learning algorithms/architectures are fundamentally the same concepts but are in different levels of a system with different context (i.e., gradient vs. tokens). … We discuss different ways of knowledge transfer between levels, resulting in unifying and generalizing concepts like meta-learning, in-context learning, recurrent neural networks, hypernetworks, etc.

2.1 重新定义：优化器即联想记忆 (Optimizer As Associative Memory)

通常我们认为梯度下降是更新权重的工具。作者证明：

Backpropagation (反向传播) 是一个联想记忆过程： 它试图将每一层的输入映射到该层的误差信号（Error Signal）
Momentum (动量) 是一个二级优化问题： 动量不是简单的滑动平均，而是一个记忆模块，试图将过去的梯度压缩到其参数中
Adam 等同于最优联想记忆： 作者证明，如果目标是预测梯度的方差（L2 回归），Adam 其实是该目标下的最优联想记忆解

2.2 重新定义：架构即嵌套优化

Transformer 是两层嵌套系统：
- Level 1 (低频/静态): 投影层（ $W_{q}, W_{k}, W_{v}$ ）和 MLP 层。它们在预训练期间更新，但在推理时是静态的。
- Level 2 (高频/动态): Attention 机制。它实际上是在每一层内部求解一个非参数回归问题（Non-parametric regression），即 In-context Learning。
结论： 所有的现代架构（Transformer, RNNs, Linear Attention）本质上都是不同更新频率和不同目标函数的联想记忆系统。

3. 方法论创新：从理论到设计

基于 NL 范式，作者提出了三个核心技术贡献：

3.1 更具表达力的优化器 (Expressive Optimizers)

既然优化器是记忆模块，我们可以把它设计得更强：

Delta Gradient Descent (DGD): 传统 SGD 是基于点积相似度的更新。作者提出了 DGD，不仅依赖当前输入，还依赖权重的状态，捕捉数据的依赖性（去除了 i.i.d 假设）。
Multi-scale Momentum Muon (M3): 作者设计了一种新的优化器M3。它结合了 Muon 优化器（正交化梯度）和多尺度动量（不同频率更新的动量项），使其能更好地捕捉长期的损失函数地形信息。

3.2 连续记忆系统 (Continuum Memory System, CMS)

针对现有 Transformer 中静态 MLP 块无法适应新知识的问题，作者提出了 CMS 来替代 MLP：

原理： CMS 不是一个简单的 MLP，而是一串更新频率不同的 MLP 块链。
机制：
- 高频 MLP（快速更新）：负责快速适应当前上下文。
- 低频 MLP（慢速更新）：负责存储持久知识。
- 这模拟了从短期记忆到长期记忆的巩固过程。
优势： 这使得模型在推理阶段（Test-time）也能更新参数，打破了训练和测试的界限。

3.3 自我修正模块：Self-Modifying Titans

作者改进了 Titans（一种现代 RNN 架构）：

Self-Referential (自我指涉)： 传统的 Attention 或 RNN 的 Key/Value 是输入的投影。Self-Modifying Titans自己生成自己的训练目标（Values），这意味着它学习“如何修改自己”。
它位于架构的最高频层，负责最高阶的上下文学习。

3.4 最终架构：HOPE

HOPE = Self-Modifying Titans (作为 Attention 替代品) + CMS (作为 MLP 替代品)

这是一个完全动态的、自我更新的“神经学习模块”。
它没有明显的“训练”和“测试”阶段，只有接收信息时的状态更新。

4. 实验结果

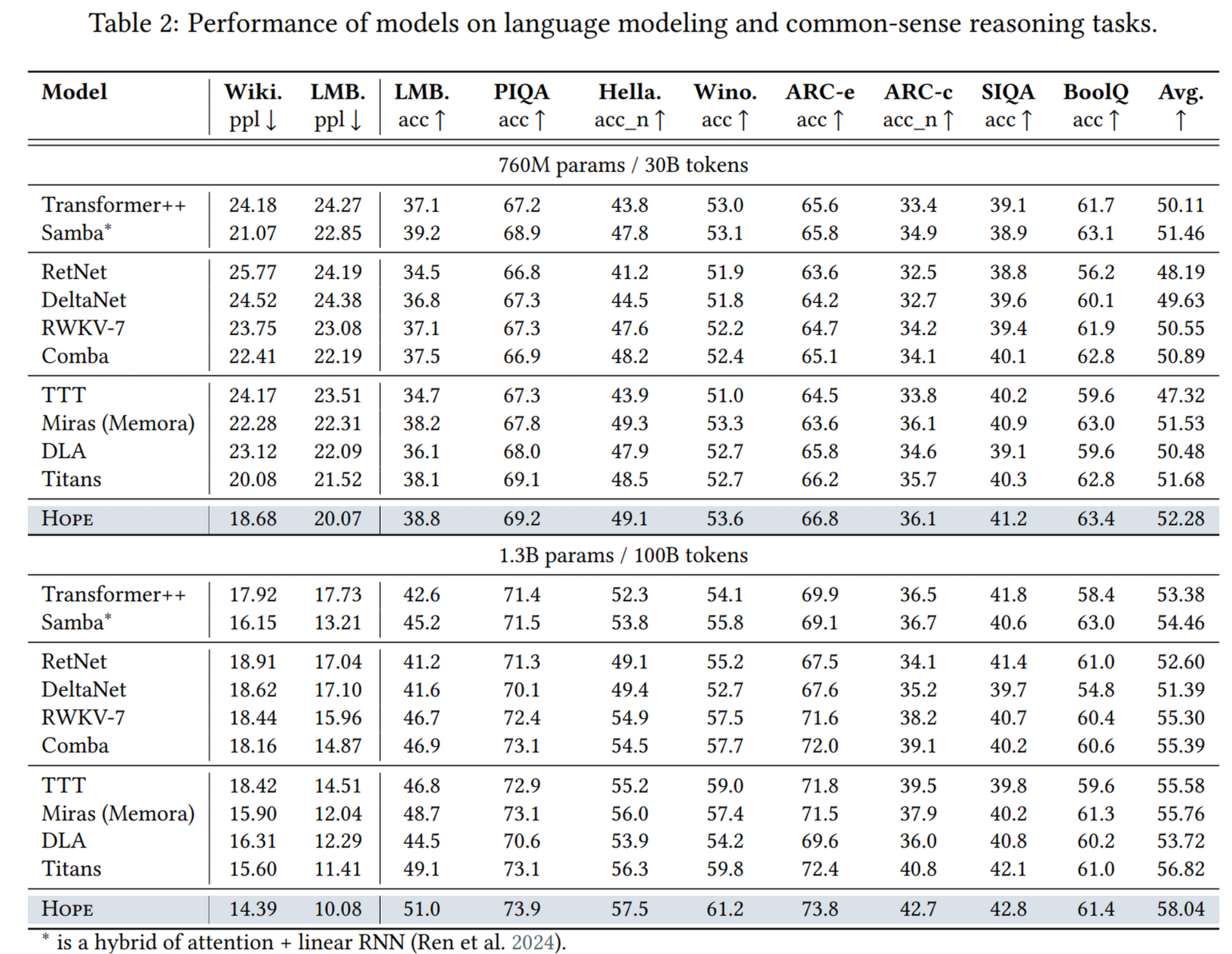
作者在多个领域进行了广泛的评估，证明了 Hope 和 NL 范式的有效性。

4.1 持续学习 (Continual Learning)

任务： 类别增量学习（Class Incremental Learning），如在文本分类中不断增加新类别。
结果： Hope 在所有基准（CLINC, Banking, DBpedia）上均超越了现有方法（包括 Elastic Weight Consolidation 和带外部学习器的 ICL）。
结论： CMS 的多频率设计有效缓解了灾难性遗忘，同时保持了对新任务的适应性

4.2 长上下文理解 (Long Context Understanding)

任务： 大海捞针（Needle-In-A-Haystack, NIAH）和 BABILong。
结果：
- Hope-Attention（使用 CMS 的 Transformer 变体）在 NIAH 的所有难度设置下都优于标准 Transformer。
- 在 BABILong（超长文本推理）中，Hope 在 1M token 长度下仍保持竞争力，而其他模型（如 Titans, ARMT）性能下降更快。
- 关键点： CMS 允许模型在处理长序列时“在线”更新记忆，从而记住更早的信息

4.3 语言建模与常识推理

基准： Wikitext, PIQA, HellaSwag 等。
结果： 在同等参数量（760M, 1.3B）下，Hope 的困惑度（Perplexity）更低，推理任务的平均准确率更高。

4.4 优化器性能

ImageNet 训练： 使用 M3 优化器训练 ViT，收敛速度和最终 Loss 均优于 AdamW 和 Muon。
效率： 虽然 M3 引入了多重动量，但在大型模型训练中，其计算效率与 AdaMuon 相当。

4.5 合成任务 (Synthetic Tasks)

任务： 形式语言识别（如奇偶校验）、复制、联想回忆。
结果： Hope 在这些任务上表现完美或接近完美，解决了 Transformer 无法处理某些非线性递归语言（如 Parity）的缺陷。

5. 局限性与讨论

尽管论文提出了极具前瞻性的框架，但也存在一些局限性：

计算开销与效率：
- CMS 意味着在推理过程中需要不断更新参数（Backprop during inference）。虽然作者设计了分块（Chunk-wise）并行策略，但这比静态权重的推理要慢，且消耗更多资源。
- M3 优化器虽然效果好，但比纯 Muon 更复杂，难以在大规模分布式训练中简单扩展。
灾难性遗忘并未彻底解决： 虽然 CMS 缓解了遗忘，但作者诚实地指出，灾难性遗忘是“压缩”的自然结果（容量有限）。NL 提供了一个缓解的路线图，而非彻底的解决方案。
复杂性： Hope 架构引入了多层级的超参数（不同块的更新频率、学习率、衰减率等），这使得调参变得更加复杂。
规模验证： 目前的实验主要集中在中小规模模型（<2B 参数）。这种动态更新的机制在千亿参数模型（如 GPT-4 级别）上的稳定性和效率仍需验证。

总结

这篇论文的核心贡献在于它打破了由于深度学习工具（如 PyTorch/TensorFlow）造成的思维定势。它告诉我们，不要把层看作静态的函数，要把它们看作动态的、有不同心跳（频率）的记忆体。Hope模型通过引入多时间尺度的自我更新机制，向着“像大脑一样持续学习”的 AI 迈出了重要一步。

数学推导

联想记忆 (Associative Memory)

定义联想记忆为一个算子 $M$ ，用于将键 $K$ 映射到值 $V$ 。最优联想记忆即为：
$M^{*} = ar g M min L (M (K), V)$
其中 $L$ 为损失函数

嵌套系统

定义一个嵌套系统由 $K$ 个有序层级（level）组成，层级高低通过更新频率來决定. 对于系统中的每一个组件 $X$ ，其更新频率 $f_{X}$ 定义为单位时间内该组件更新的次数.

若 $f_{A} > f_{B}$ ，则记为 $A$

优化器是一种联想记忆

考虑神经网络 $W$ ，输入 $x_{t}$ 时的权重为 $W_{t}$ ，损失函数为 $L$ 。

梯度下降

对于梯度下降法，有

W_{t + 1} = W_{t} - η \nabla_{W_{t}} L (W_{t}; x_{t})

在单层 MLP 情况下，记 $y_{t} = W_{t} x_{t}$ 由于

\nabla_{W_{t}} L (W_{t}; x_{t}) = \nabla_{y_{t}} L (y_{t}) \cdot \nabla_{W_{t}} (W_{t} x_{t}) = \nabla_{y_{t}} L (y_{t}) x_{t}^{⊤}

将其转化为近端梯度形式即为：

W_{t + 1} = ar g W min (⟨ W x_{t}, \nabla_{y} L ⟩ + \frac{1}{2 η} ∥ W - W_{t} ∥_{2}^{2})

于是可以将梯度下降法视为求解：

算子为线性变换 $M$ ，键为每个时间步 $t$ 的输入 $x_{t}$ ，值为梯度 $\nabla_{y} L$ ，损失函数为内积

的最优联系记忆. 据此我们可以知道，可以将模型权重视为将输入 $x$ 和误差 $\nabla_{y} L$ 进行映射的一个联想记忆. 可以理解为：对那些会引起较大模型变化的（局部意外信号，Local Surprise Signal, LSS，量化了当前模型输出与目标函数所期望的结构之间的不匹配程度。）的输入，模型参数会更加记忆其带来的变化. 这是一个**单层级（1-level）**的学习系统。

动量

动量的定义为：

m_{t + 1} W_{t + 1} = β m_{t} + \nabla_{W_{t}} L (W_{t}; x_{t}) = W_{t} - η m_{t + 1}

可以将这看作一个二阶的嵌套优化问题，动量 $m_{t}$ 的含义即为

m_{t + 1} \approx ar g m min (i = 1 \sum t ⟨ m, - \nabla_{y} L_{i} ⟩ + \frac{1}{2 ( 1 - β )} ∥ m - m_{t} ∥^{2})

这说明带动量的梯度下降为一个双层级（2-level） 的缔合记忆系统：

内层（Inner Level）：动量项 $m_{t}$ 本身是一个无键（key-less）的缔合记忆。它通过优化上述目标函数，将历史梯度 ${\nabla_{W_{t}} L}$ 压缩到其参数 $m$ 中。这是一个快速更新的记忆
外层（Outer Level）：权重 $W_{t}$ 是慢速更新的记忆。它利用内层记忆 $m_{t + 1}$ 的输出来进行更新

这其实是 fast weight programmers (FWP) 的思想，将优化器本身也看作一个学习模块，有自己的目标函数和记忆状态。慢速网络 $W_{t}$ 的权重更新由一个快速网络 $m_{t}$ 生成

Adam

见原论文 Appendix B 的推导。

模型架构也可以是联想记忆

以线性注意力为例：

k_{t} = x_{t} W_{k}, q_{t} = x_{t} W_{q}, v_{t} = x_{t} W_{v} M_{t} = M_{t - 1} + v_{t} k_{t}^{⊤} y_{t} = M_{t} q_{t}

同样可以被看作一个双层级的优化过程：

内层（Inner Level）：注意力记忆 $M_{t}$ 的更新。这是一个快速过程，在每个时间步都发生，旨在将当前的键值对 $(k_{t}, v_{t})$ 压缩进记忆状态 $M_{t}$ 。
外层（Outer Level）：投影矩阵 $W_{k}, W_{v}, W_{q}$ 的训练。这是一个慢速过程，旨在学习如何从输入 $x_{t}$ 中提取有效的键、值和查询。

如何定义层级

上面我们多次提到某某结构是“外层”，某某是“内层”，但如何判定呢？使用更新频率來判断。称组件 $A$ 比组件 $B$ 快，当且仅当：

$f_{A} > f_{B}$ ，或者
$f_{A} = f_{B}$ ，且更新 $B$ 前必须先更新 $A$

通过这个定义，一个机器学习模型可以被唯一地表示为一个有序的层级集合。层级越高，其组件的更新频率越低。每个组件都有其自身的优化问题和上下文流。

在此视角下，transformer 架构可以看成由高频层（Attention，理论上为 $\infty$ ）和低频层（ffn，推理时为 $0$ ，训练时为 $1$ ）构成，两个层级的功能和更新速率差异巨大，中间存在巨大的空白；据此作者才提出 HOPE 架构以弥补更新频率间的空白

Kinnari

探索

Nested Learning: The Illusion of Deep Learning Architecture

1. 核心 Insight 与神经科学动机

1.1 核心批判：深度学习的“错觉”与“失忆”

1.2 神经科学启发：多时间尺度处理

2. 理论框架：嵌套学习 (Nested Learning)

2.1 重新定义：优化器即联想记忆 (Optimizer As Associative Memory)

2.2 重新定义：架构即嵌套优化

3. 方法论创新：从理论到设计

3.1 更具表达力的优化器 (Expressive Optimizers)

3.2 连续记忆系统 (Continuum Memory System, CMS)

3.3 自我修正模块：Self-Modifying Titans

3.4 最终架构：HOPE

4. 实验结果

4.1 持续学习 (Continual Learning)

4.2 长上下文理解 (Long Context Understanding)

4.3 语言建模与常识推理

4.4 优化器性能

4.5 合成任务 (Synthetic Tasks)

5. 局限性与讨论

总结

数学推导

优化器是一种联想记忆

梯度下降

动量

Adam

模型架构也可以是联想记忆

如何定义层级

Reference

关系图谱

目录

反向链接

最近的笔记

Optimizing Test-Time Compute via Meta Reinforcement Fine-Tuning

Beyond Autoregression: Discrete Diffusion for Complex Reasoning and Planning

Fedora 环境搭建记录

Kinnari

探索

Nested Learning: The Illusion of Deep Learning Architecture

1. 核心 Insight 与 神经科学动机

1.1 核心批判：深度学习的“错觉”与“失忆”

1.2 神经科学启发：多时间尺度处理

2. 理论框架：嵌套学习 (Nested Learning)

2.1 重新定义：优化器即联想记忆 (Optimizer As Associative Memory)

2.2 重新定义：架构即嵌套优化

3. 方法论创新：从理论到设计

3.1 更具表达力的优化器 (Expressive Optimizers)

3.2 连续记忆系统 (Continuum Memory System, CMS)

3.3 自我修正模块：Self-Modifying Titans

3.4 最终架构：HOPE

4. 实验结果

4.1 持续学习 (Continual Learning)

4.2 长上下文理解 (Long Context Understanding)

4.3 语言建模与常识推理

4.4 优化器性能

4.5 合成任务 (Synthetic Tasks)

5. 局限性与讨论

总结

数学推导

优化器是一种联想记忆

梯度下降

动量

Adam

模型架构也可以是联想记忆

如何定义层级

Reference

关系图谱

目录

反向链接

最近的笔记

Optimizing Test-Time Compute via Meta Reinforcement Fine-Tuning

Beyond Autoregression: Discrete Diffusion for Complex Reasoning and Planning

Fedora 环境搭建记录

1. 核心 Insight 与神经科学动机