Optimizing Test-Time Compute via Meta Reinforcement Fine-Tuning

[2503.07572] Optimizing Test-Time Compute via Meta Reinforcement Fine-Tuning

Optimizing LLM Test-Time Compute Involves Solving a Meta-RL Problem

TL;DR

本文针对现有大模型（如 DeepSeek-R1）在扩展测试时计算（Test-Time Compute）时效率低下且缺乏过程指导的问题，提出了 MRT (Meta Reinforcement Fine-Tuning) 框架。该方法将推理过程重新形式化为元强化学习问题，不同于仅奖励最终答案的传统 RL（如 GRPO），MRT 引入了基于“进度（Progress）”的密集奖励，激励模型在思维链的每一步都实质性地提升解题概率，从而最小化“累积遗憾”。实验证明，MRT 在数学推理任务上相比标准 RL 方法，不仅带来了 2-3 倍的相对准确率提升，更实现了 1.5 倍以上的 Token 效率飞跃，成功让模型在消耗更少计算资源的情况下达到更优的推理性能。

$P$.$S$. 我觉得图画得特别好看，值得学一学

1. 核心背景与动机 (Introduction & Motivation)

现状： 近期 DeepSeek-R1 和 OpenAI o1 等模型证明，通过增加测试时的计算量（即让模型产生更长的思维链 CoT），可以显著提升推理能力。 问题： 当前的主流方法主要依赖 基于结果的强化学习（Outcome-reward RL），即只有当最终答案正确时才给予奖励（0/1 奖励）。作者指出了这种方法的两个主要缺陷：

1. 效率低下： 模型倾向于生成不必要的冗长思维链，或者只是在“撞大运”，并没有真正利用中间的 Token 取得实质性进展。
2. 缺乏过程激励： 只有最终结果有奖励，模型无法区分“方向正确但最后一步错了”和“完全胡说八道”的区别。
3. 遗憾（Regret）未被最小化： 现有的长思维链模型（如 DeepSeek-R1）并未在思维过程中最大化“进度”。

核心洞察： 作者将测试时的思维过程重新形式化为一个 元强化学习（Meta-RL） 问题。

• 把模型在测试时生成的每一个思维片段（Episode）看作是一个“探索”过程。
• 一个优秀的模型应该在这个过程中表现出最佳的“探索 - 利用”（Explore-Exploit）平衡。
• 目标不应仅仅是最终做对，而是要最小化累积遗憾（Cumulative Regret），即在每一个思维步骤上，都要尽可能缩短与正确答案之间的距离。

---

2. 理论框架：元强化学习与累积遗憾 (Theoretical Framework)

这是文章最核心的理论创新点。

2.1 定义“累积遗憾” (Cumulative Regret)

作者提出，衡量测试时计算是否高效，应该看 Cumulative Regret。

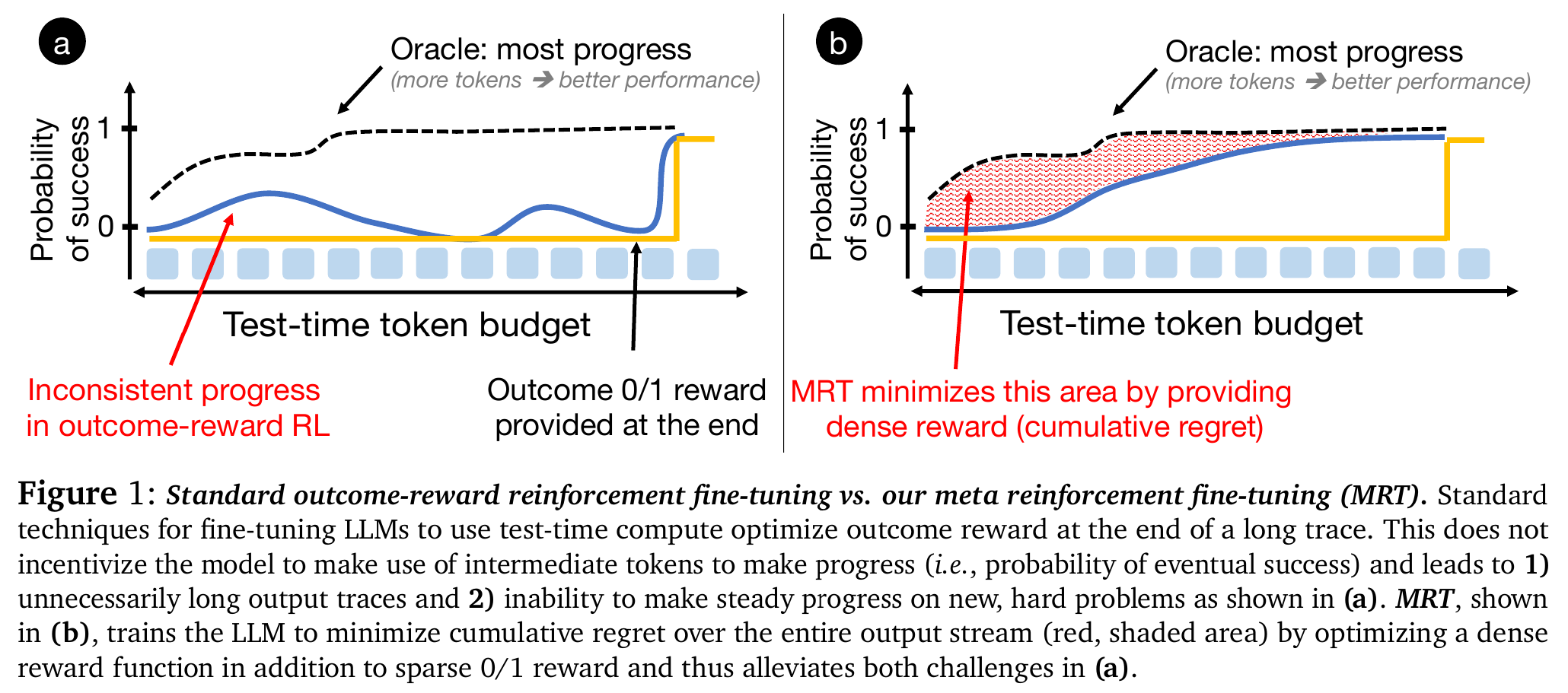
• 直观理解： 见 Figure 1。
  • 图 1(a) Outcome-reward RL： 模型的成功率（蓝色曲线）在生成很多 Token 后仍然很低，直到最后突然跳升。红色阴影面积（遗憾）很大
  • 图 1(b) MRT (本文方法)： 模型每生成一段 Token，成功率就稳步上升。红色阴影面积（遗憾）被最小化
• 数学定义：

$${\Delta }_k^{\mu }(x;\pi )={\mathbb{E}}_{z\sim \pi }\left[\sum _{j=0}^{k-1}(J_r(x;{\pi }_j^{\ast })-J_r(x;\mu (\cdot |x,z_{0:j})))\right]$$

其中，${\pi }_j^{\ast }$ 是最优策略（Oracle），$\mu$ 是当前模型对最终答案的估计。

2.2 定义“进度” (Progress) 作为密集奖励

由于无法直接计算“遗憾”（因为不知道 Oracle），作者提出最大化 Progress（进度） 来作为替代目标。

Progress 定义 (Definition 6.1): 给定当前的思维上下文 $c$ 和新生成的片段 $z_j$，进度定义为：

$$r_{prg}^{\mu }(z_j;c):=J_r(\mu (\cdot |z_j,c))-J_r(\mu (\cdot |c))$$

解释： 生成片段 $z_j$ 后，模型 $\mu$ 猜对答案的概率，减去生成前猜对的概率。如果这个差值是正的，说明这个片段是有用的，让模型离真理更近了一步。

---

3. 方法论：MRT (Meta Reinforcement Fine-Tuning)

MRT 的核心思想是：除了最终的 0/1 结果奖励外，引入基于 Progress 的密集奖励（Dense Reward）。

3.1 两种实现变体

作者提出了两种实例化 MRT 的方法，分别对应离线微调和在线强化学习：

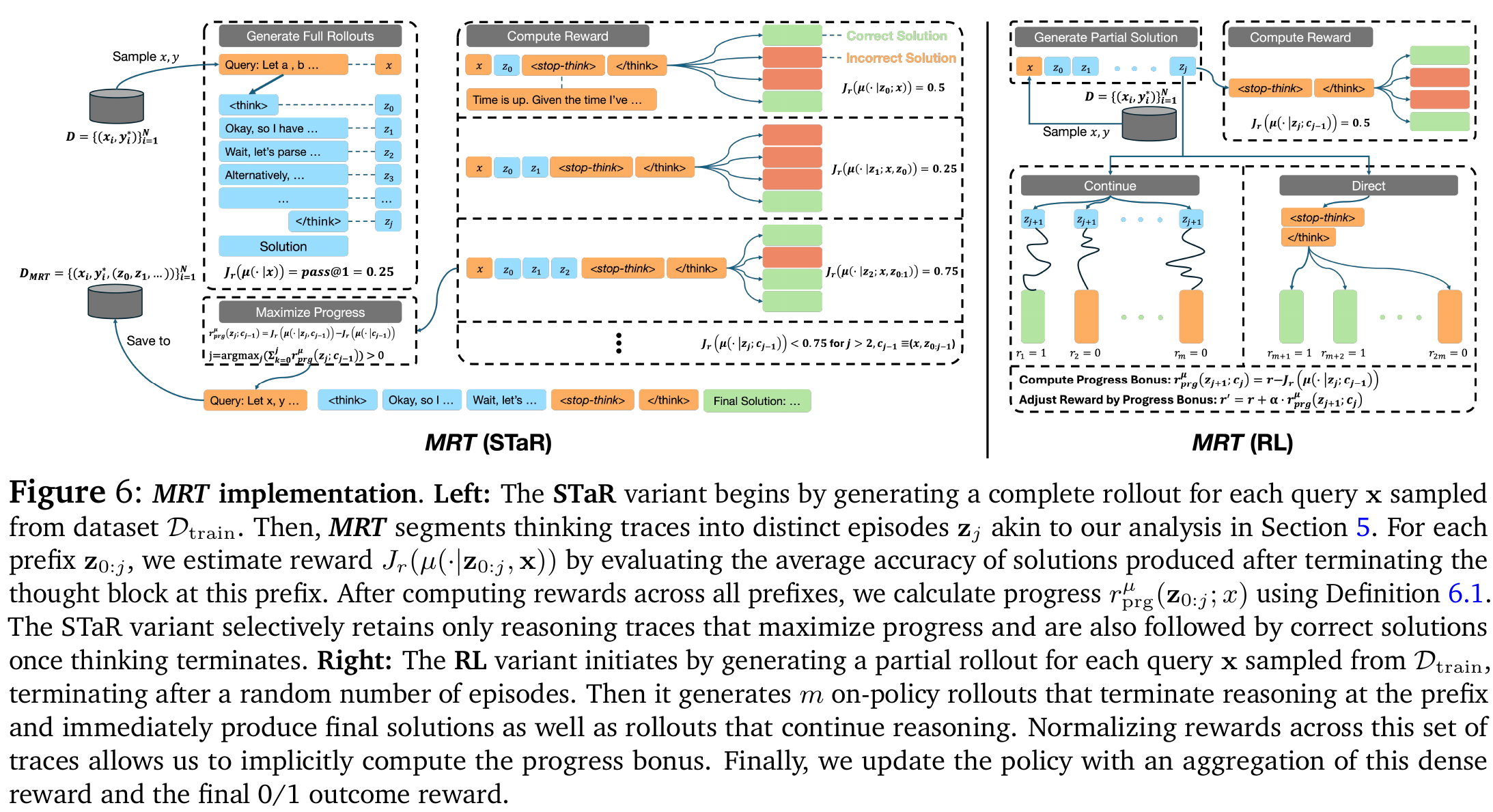
1. MRT (STaR) - 类似 Rejection Sampling：
   • 利用基础模型生成多个完整的推理轨迹。
   • 将轨迹切分为多个 Episodes（例如按 <think> 标签或换行符）。
   • 计算每个前缀的 Progress（看在这个前缀下，模型直接回答的正确率是否提升）。
   • 筛选策略： 只保留那些既最终正确、又在过程中最大化了 Progress 的轨迹。
   • 使用这些高质量轨迹进行监督微调（SFT）。
2. MRT (RL) - 类似 GRPO/PPO：
   • 使用在线强化学习算法（如 GRPO）。
   • 奖励函数设计： $R=r_{outcome}+\alpha \cdot \sum r_{prg}$，即最终奖励 + 进度奖励的加权和
   • 具体操作： 在训练过程中，模型生成部分思维链后，会通过一个 Meta-Prover $\mu$（通常是强制模型立即停止思考并给出答案）来评估当前的胜率，以此计算 Progress 奖励。

3.2 两种应用场景

1. 开放式生成（Open-ended）： 类似 DeepSeek-R1，包含 <think> 标签，内容不受限
2. 回溯搜索（Backtracking Search）： 强制模型执行“生成 → 发现错误 → 回溯 → 修改”的结构化步骤

---

4. 实验配置 (Experimental Setup)

• 基础模型：
  • DeepScaleR-1.5B-Preview
  • DeepSeek-R1-Distill-Qwen-1.5B
  • DeepSeek-R1-Distill-Qwen-7B
  • Llama-3.1-8B-Instruct (用于回溯搜索实验)
• 数据集：
  • 训练：NuminaMath (从中采样 10k 或 4k 个问题)。
  • 测试：AIME 2024, AIME 2025, AMC 2023, MinervaMATH, MATH500。
• 基线对比：
  • Outcome-reward RL (GRPO)： 仅使用最终结果奖励的标准 RL。
  • Length Penalty： 带有长度惩罚的 RL（试图通过惩罚长输出来提高效率）。
  • Direct / SFT： 直接微调。
  • RISE / STaR： 其他自修正或自举方法。

5. 实验结果 (Experimental Results)

5.1 准确率提升 (Table 1)

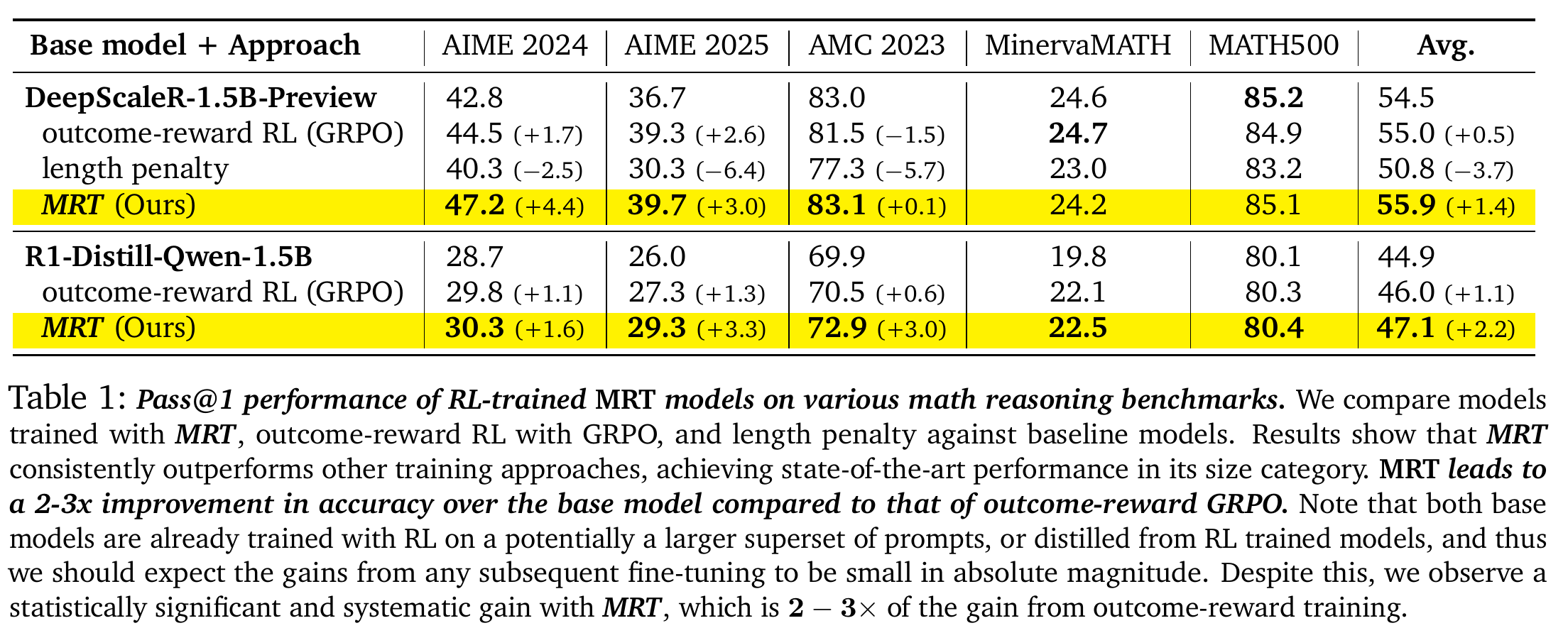
MRT 在多个数学基准测试上均超越了 Outcome-reward RL (GRPO)。

• DeepScaleR-1.5B 基础模型： MRT 平均准确率 55.9%，优于 GRPO 的 55.0%。在 AIME 2024 上，MRT 提升了 4.4%，而 GRPO 仅提升 1.7%。
• DeepSeek-R1-Distill-Qwen-1.5B： MRT 平均 47.1%，优于 GRPO 的 46.0%
• 关键结论： MRT 带来的相对性能提升是 Outcome-reward RL 的 2-3 倍。

5.2 Token 效率 (Token Efficiency) - Figure 7 & 8

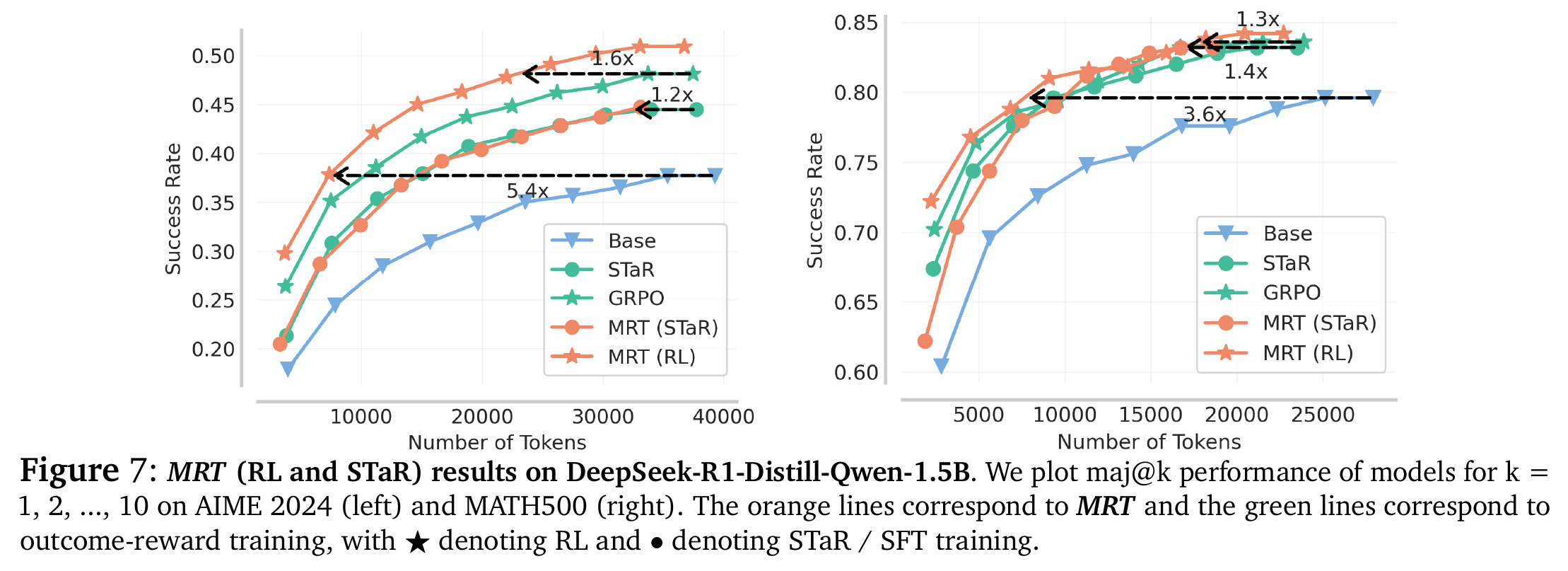
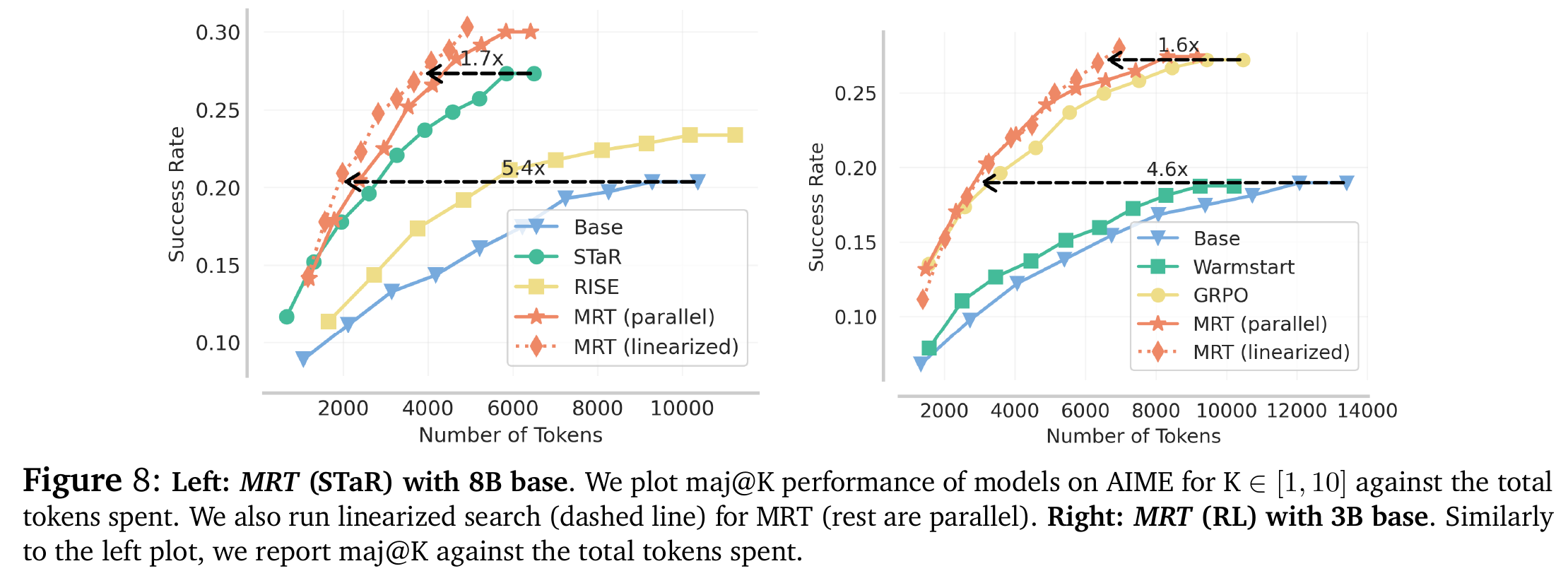这是 MRT 最显著的优势。

• 更少的 Token，更高的分： 在达到相同准确率的情况下，MRT 需要的 Token 数量远少于基线。
• 数据支撑：
  • 在 AIME 2024 上，MRT 相比 GRPO 提高了 1.2-1.6 倍 的 Token 效率
  • 相比 Base 模型，MRT 仅需 1/5 的 Token 量即可达到同等性能
• 长度惩罚的对比： 显式地惩罚长度（Length Penalty）虽然能缩短输出，但会显著降低准确率（Table 1 中下降了 3.7%）。MRT 在缩短长度的同时反而提高了准确率。

5.3 泛化与外推 (Extrapolation) - Figure 9 & 29

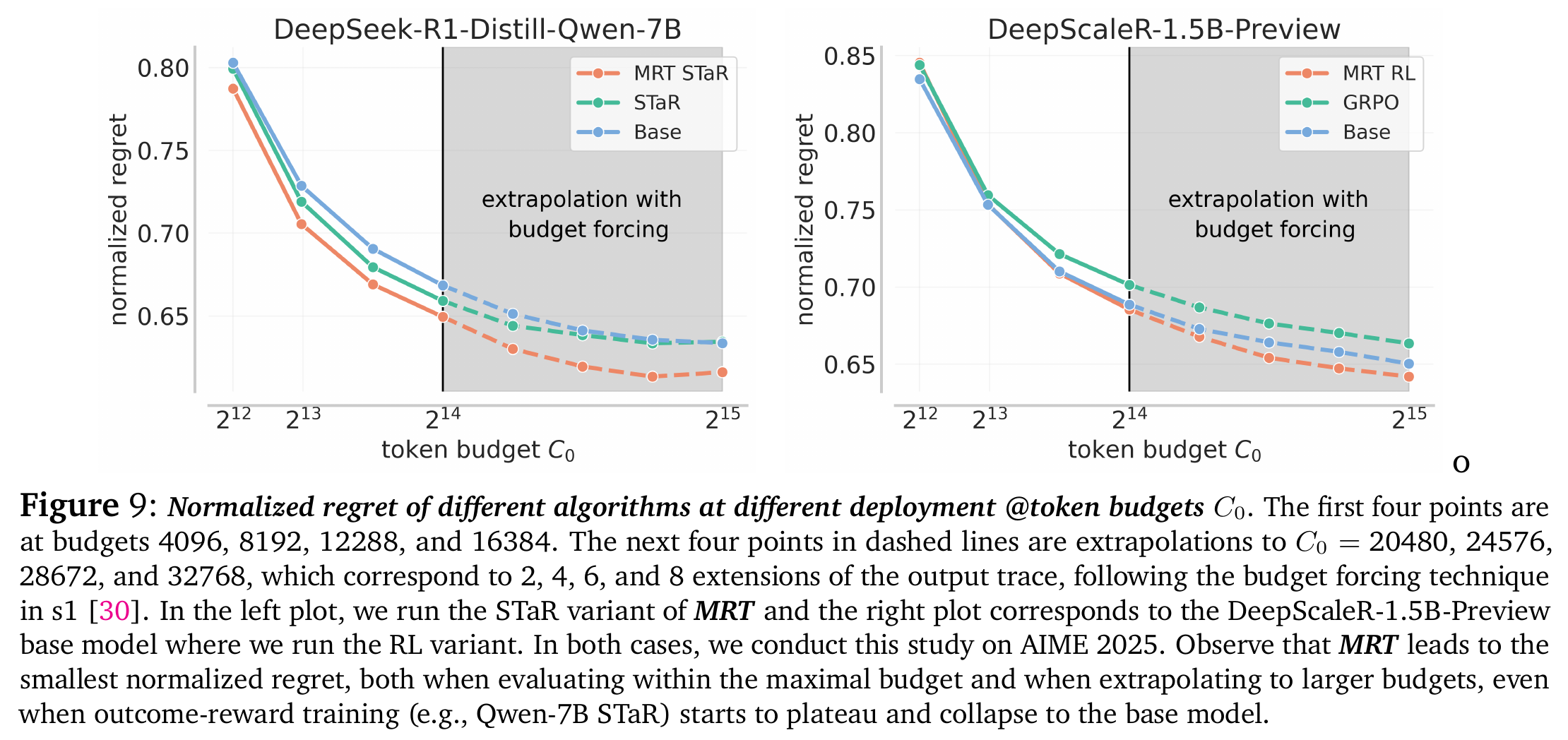
• Budget-Agnostic（预算无关性）： MRT 训练出的模型在测试时，即使给予比训练时更多的 Token 预算，也能持续提升性能，表现出更低的 Normalized Regret
• 相比之下，Outcome-reward RL 训练的模型在超出训练长度后，性能往往会饱和甚至下降。

5.4 对 DeepSeek-R1 的案例分析 (Section 5 & Figure 3)

作者专门分析了 DeepSeek-R1-Distill-32B。

• 发现： R1 并没有最小化遗憾。随着思维链变长，它的成功率并没有稳步提升（Figure 3 中的蓝色曲线增长缓慢）。
• 对比： 如果在中间步骤强制停止并进行多数投票（Majority Voting），效果反而比让 R1 继续想下去更好。这说明 R1 的长思维链中存在大量低效计算

5.5 训练过程中的长度演变 (Ablation Study)

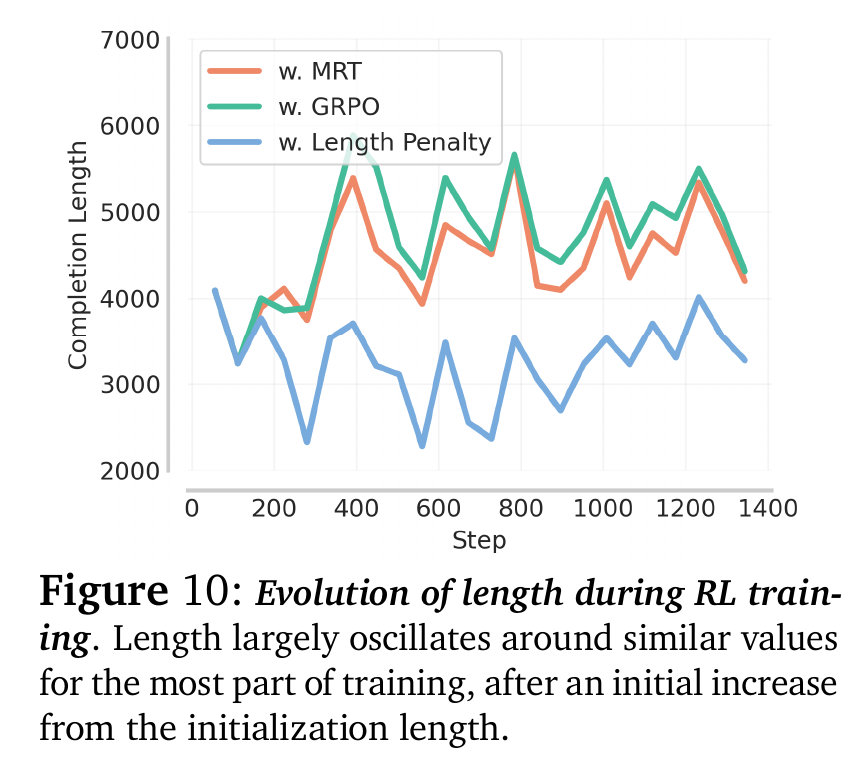
• Figure 10: MRT 训练过程中，模型输出长度会略微下降，但这是一种“健康的缩短”，去除了无效的思考。
• 关于 Curriculum（课程学习）的解释： 之前有研究（如 DeepScaleR）发现先用短上下文（8K）训练再扩展到长上下文（16K）效果好。本文用 MRT 理论解释了这一点：短上下文训练阶段迫使模型在有限预算内最大化 Progress，从而学到了更高效的思考策略。

---

6. 总结与贡献 (Conclusion)

1. 新视角： 将测试时计算优化形式化为 Meta-RL 问题，并引入 累积遗憾 作为衡量标准。
2. 新方法 MRT： 提出了一种通用的微调范式，通过奖励 Progress（逐步的成功率提升） 而不仅仅是最终结果，来训练更高效的推理模型。
3. SOTA 性能： 在 1.5B - 8B 参数规模上，MRT 在准确率和 Token 效率上双双击败了当前最强的 Outcome-reward RL（如 GRPO）。
4. 揭示了现有模型的低效： 指出 DeepSeek-R1 等模型虽然强大，但在 Token 利用效率上仍有巨大优化空间（即它们常常是在浪费计算资源）。

这篇文章的核心价值在于它不仅为了刷榜，而是从理论高度解释了“为什么长思维链有效”以及“如何让它更有效”，为未来的 Scaling Test-Time Compute 指明了方向——不仅要想得久，还要想得每一步都有进度。