FlowRL: Matching Reward Distributions for LLM Reasoning

https://arxiv.org/abs/2509.15207

TL;DR

提出了一种新的大语言模型（LLM）强化学习（RL）范式：FlowRL。它不再单纯追求“奖励最大化”（Reward Maximization），而是转向“奖励分布匹配”（Reward Distribution Matching）。

1. 核心 Insight 与 动机 (Motivation)

现有方法的局限性

目前的推理模型（如 DeepSeek-R1 等）主要依赖基于奖励最大化的 RL 算法，例如 PPO (Proximal Policy Optimization) 或 GRPO (Group Relative Policy Optimization)。

• Mode Collapse（模式坍塌）： 这些算法倾向于寻找并过度优化获得最高奖励的那一条路径（Dominant Mode）。
• 缺乏多样性： 模型会忽略那些发生频率较低但依然正确、逻辑合理的推理路径。
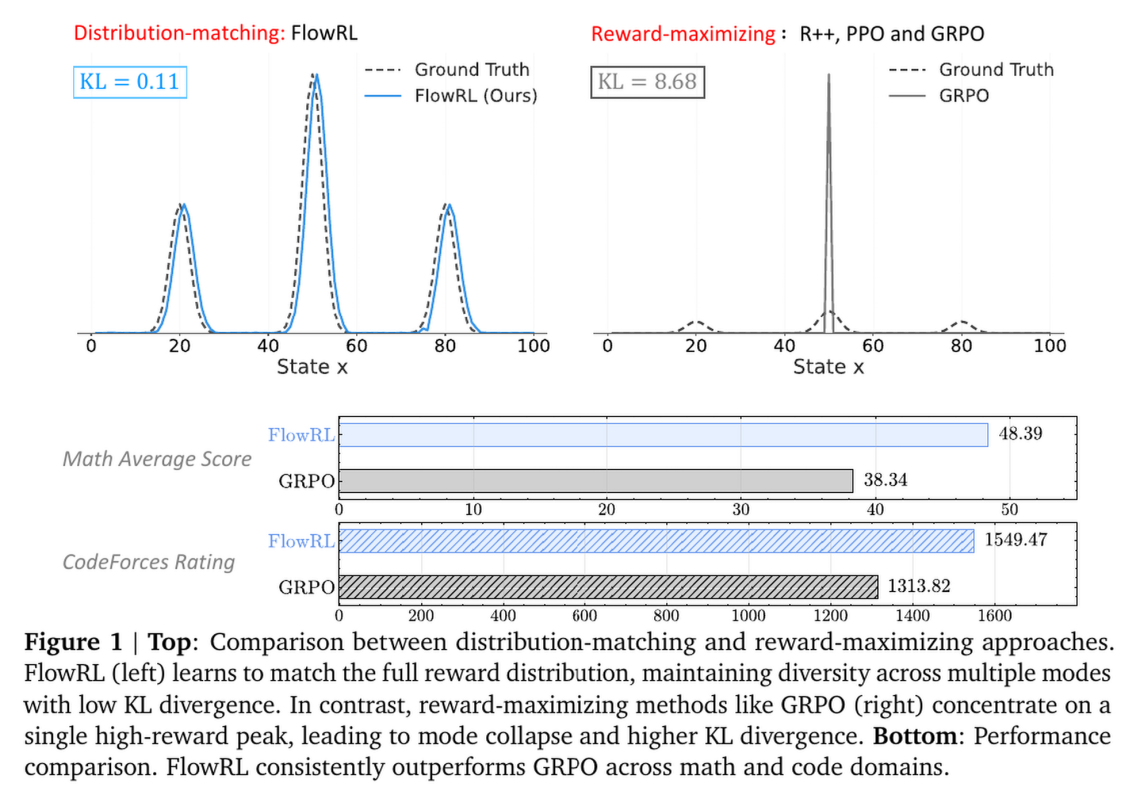
• 泛化性差： 正如论文 Figure 1 所示，GRPO 容易陷入局部最优（如死记硬背某种解题套路），一旦该套路失效，模型就无法解题。而多样化的探索对于解决复杂的长链条推理（CoT）至关重要。

FlowRL 的核心思想

FlowRL 的目标不是寻找“最大值”，而是进行分布匹配。

• 目标分布： 将标量奖励 $r$ 转化为一个目标概率分布。如果路径 A 的奖励是 10，路径 B 的奖励是 5，FlowRL 希望模型生成 A 的概率大致是 B 的两倍（指数级比例），而不是只生成 A 不生成 B。
• 理论基础： 借鉴了 GFlowNets (Generative Flow Networks) 的流平衡（Flow Balance）思想。
• 效果： 通过学习匹配整个奖励分布，模型能保持推理的多样性，探索出更多不同的解题策略，从而显著提高泛化能力。

2. 方法论 (Methodology)

2.1 从 KL 散度到轨迹平衡 (Trajectory Balance)

FlowRL 的目标是最小化策略分布 ${\pi }_{\theta }(y|x)$ 与目标分布之间的 逆向 KL 散度 (Reverse KL)

$$\underset{\theta }{\min }{D}_{\text{KL}}\left({\pi }_{\theta }(\mathbf{y}\mid \mathbf{x})\parallel \frac{\exp (\beta r(\mathbf{x},\mathbf{y}))}{Z_{\varphi }(\mathbf{x})}\right)$$

• $Z_{\varphi }(\mathbf{x})$ 是一个可学习的配分函数（Partition Function），用于将奖励归一化为概率分布。
• Proposition 1（关键理论）： 论文证明，最小化上述 KL 散度，在梯度期望上等价于最小化 GFlowNet 中的 轨迹平衡损失 (Trajectory Balance Loss)：

$${\mathcal{L}}_{TB}=(\log Z_{\varphi }(\mathbf{x})+\log {\pi }_{\theta }(\mathbf{y}\mid \mathbf{x})-\beta r(\mathbf{x},\mathbf{y}){)}^2$$

2.2 针对长 CoT 推理的改进

直接将 GFlowNet 的损失函数应用于 LLM 长文本推理（CoT 可能长达 8k token）会遇到两个严重问题：

1. 梯度爆炸 (Gradient Explosion)：
   • $\log {\pi }_{\theta }(\mathbf{y}\mid \mathbf{x})$ 是所有 token 对数概率的和。对于长序列，这个值会非常大（负数绝对值大），导致梯度不稳定。
   • 解决方案：长度归一化 (Length Normalization)。将对数概率除以序列长度 $|\mathbf{y}|$，即 $\frac{1}{|\mathbf{y}|}\log {\pi }_{\theta }$。
2. 采样不匹配 (Sampling Mismatch)：
   • GFlowNet 通常要求 On-policy（在线）采样。但为了训练效率，主流 RL（如 PPO/GRPO）使用 Importance Sampling（重要性采样）来复用旧策略 ${\pi }_{\text{old}}$ 生成的数据。
   • 解决方案：引入重要性采样 (Importance Sampling)。类似于 PPO，引入比率 $w=\frac{{\pi }_{\theta }}{{\pi }_{\text{old}}}$ 并进行截断（Clip），以纠正分布偏差并稳定训练。

2.3 最终的 FlowRL 目标函数

结合上述改进，FlowRL 的最终损失函数如下（Eq. 6）：

$${\mathcal{L}}_{\text{FlowRL}}=w\cdot {\left(\log Z_{\varphi }(\mathbf{x})+\frac{1}{|\mathbf{y}|}\log {\pi }_{\theta }(\mathbf{y}\mid \mathbf{x})-\beta \hat{r}(\mathbf{x},\mathbf{y})-\frac{1}{|\mathbf{y}|}\log {\pi }_{\text{ref}}(\mathbf{y}\mid \mathbf{x})\right)}^2$$

• $Z_{\varphi }(\mathbf{x})$：由一个简单的 3 层 MLP 预测，输入是 Prompt 的 hidden states 均值。
• $\hat{r}$：经过 Group Normalization 的奖励。
• ${\pi }_{\text{ref}}$：参考模型（预训练模型），作为先验约束加入奖励中（防止模型崩坏）。

3. 实验设置 (Experiment Settings)

• 基座模型： Qwen2.5-7B/32B (数学任务), DeepSeek-R1-Distill-Qwen-7B (代码任务)。
• 基线对比 (Baselines)： REINFORCE++ (R++), PPO, GRPO。
• 数据集：
  • 数学： AIME 2024/2025, AMC 2023, MATH-500, Minerva, Olympiad。
  • 代码： LiveCodeBench, CodeForces, HumanEval+。
• 配置： 使用 veRL 框架，每个 Prompt 生成 8 条回复 (Group Size = 8)。

4. 实验结果 (Results)

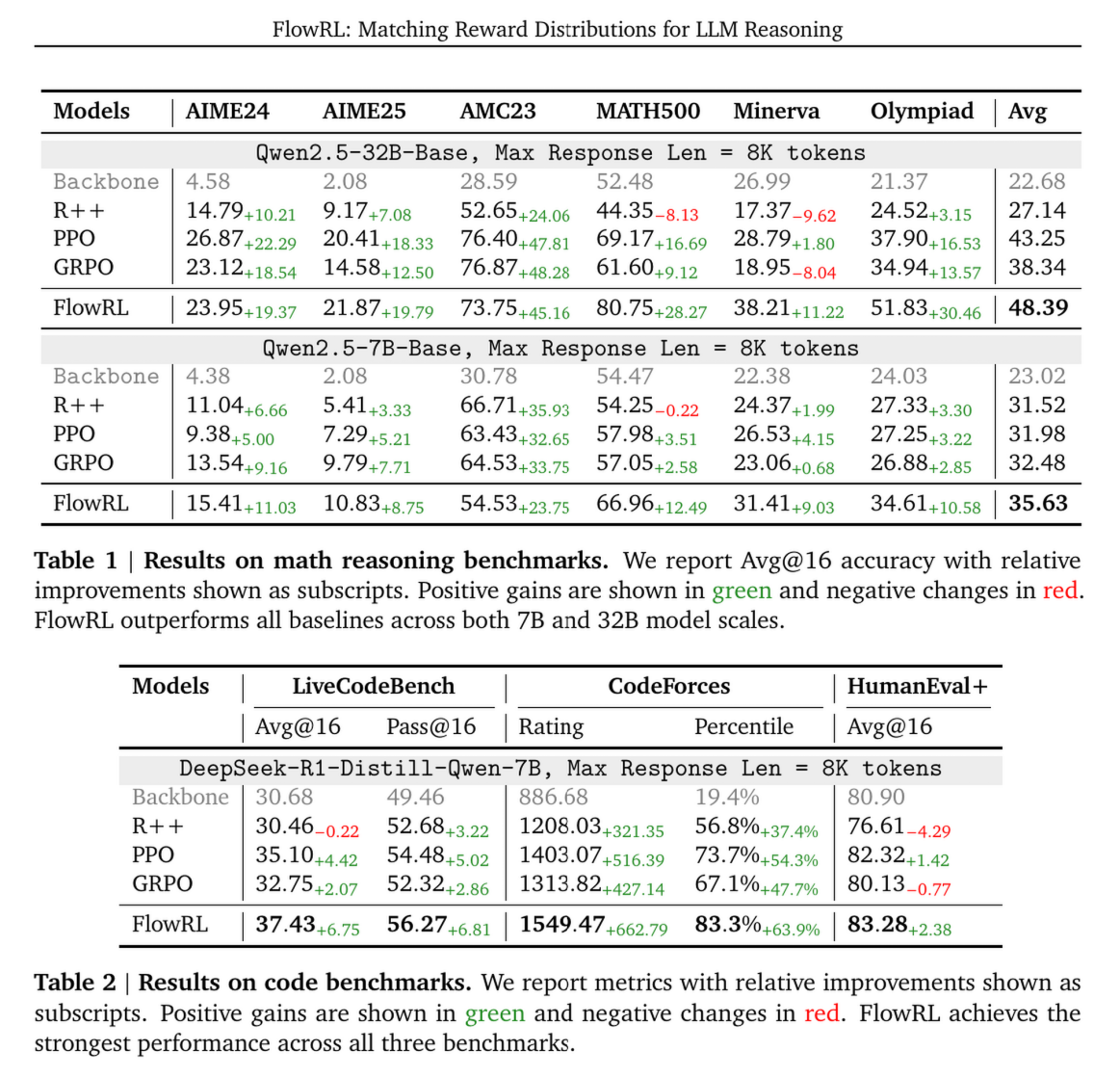
4.1 数学推理 (Math Reasoning)

• 整体提升：
  • 在 Qwen2.5-32B 上，FlowRL 平均分达到 48.39%。
  • 相比 GRPO (38.34%) 提升了 10.0%。
  • 相比 PPO (43.25%) 提升了 5.1%。
• 难点突破： 在高难度的奥数题（如 AIME, Olympiad）上提升尤为明显。例如 AIME25 上，FlowRL 得分 21.87，而 GRPO 仅为 14.58。

4.2 代码推理 (Code Reasoning)

• FlowRL 在 CodeForces, LiveCodeBench 等榜单上全面超越 GRPO。
• CodeForces Rating： FlowRL 达到 1549.47，而 GRPO 为 1313.82，PPO 为 1403.07。这显示了其在逻辑极其严密的编程任务中强大的泛化能力。

4.3 多样性分析 (Diversity Analysis) - 非常重要的 Insight

论文通过 Case Study（Figure 4 & Table 4）深入分析了模型行为：

• GRPO 的失败案例： 在一道 AIME 题目中，GRPO 陷入了死循环。它反复尝试使用“均值不等式 (AM-GM)”这一单一技巧，导致导出矛盾结论（$a=b=c$），无法解题。这是典型的 Mode Collapse。
• FlowRL 的成功： FlowRL 探索了多种路径，包括设 $a=b$ 利用对称性、构造三次方程、有理根测试等，最终解出了题目。
• 量化指标： 使用 GPT-4o-mini 对生成的 16 个解进行多样性打分，FlowRL 的多样性得分显著高于 PPO 和 GRPO。

4.4 消融实验 (Ablation Studies)

• 重要性采样 (IS) 的作用： 如果去掉 Importance Sampling，FlowRL 的性能从 35.63% 暴跌至 26.71%。这证明了解决“采样不匹配”问题对于将 GFlowNet 思想应用于离线/以数据为中心的 RL 训练至关重要。
• 超参数 $\beta$： 设置为 15 时效果最佳。

5. 总结与评价

• 核心贡献： 论文证明了在 LLM 推理任务中，“匹配奖励分布”比“最大化奖励”更有效。
• 方法创新： 成功将 GFlowNet 的轨迹平衡（Trajectory Balance）理论适配到了长文本生成的 RL 场景中，通过长度归一化和重要性采样解决了工程落地的痛点。
• 理论联系： 论文还在附录中证明了 FlowRL 本质上是在联合最大化期望奖励和策略熵（Max Entropy RL），这解释了为什么它能兼顾性能与多样性。

总的来说，FlowRL 为 LLM 的 Post-training 提供了一个比 PPO/GRPO 更稳健、更能促进探索（Exploration）的新方向，特别适合需要复杂多步推理的场景。