Thinker: Learning Fast and Slow

TL;DR

论文的核心思想是受到心理学中**双重加工理论（Dual Process Theory）**的启发，提出了一种新的强化学习（RL）训练范式——Thinker Task。该任务将大语言模型（LLM）的推理过程分解为四个特定的阶段（快思考、验证、慢思考、总结），旨在分别训练模型的直觉、评估、推理和归纳能力，从而解决当前 LLM 推理（如 CoT）中存在的低效、冗余和信用分配不精确的问题。

1. 核心动机与背景

• 现状： 现有的研究表明，通过强化学习（如 DeepSeek R1）可以提升 LLM 在数学和代码任务上的推理能力。模型在长思维链（CoT）中展现出了“自修正”的涌现能力。
• 问题：
  1. 效率低下： 自修正往往伴随着大量的回溯和冗余，导致推理过程非常长且混乱。
  2. 信用分配（Credit Assignment）低效： 在传统的 RL 训练（如 GRPO）中，如果最终答案正确，整个推理序列都会得到正向奖励。这导致模型可能会奖励那些无效的搜索路径或不确定的验证步骤，只要最后蒙对了就行。
  3. 缺乏针对性： 模型的“直觉”（快速找到正确路径的能力）和“验证”（自信地评估路径的能力）没有被显式地训练。

2. 提出的算法：Thinker Task (思考者任务)

作者提出了一种全新的单一对话多步任务结构，将 QA（问答）过程分解为四个步骤。这不仅仅是提示词工程（Prompt Engineering），而是环境增强（Environment Augmentation），即通过修改 RL 环境的交互方式来训练模型。

2.1 四个阶段详解

整个过程在一个对话历史中进行。

1. 第一步：快思考 (Fast Thinking - System 1)
   • 任务： 在严格的 Token 预算（如 1000 tokens）内给出简洁的答案。
   • 动机： 训练模型的直觉。因为预算有限，模型无法进行广泛搜索，必须依赖直觉找到最有希望的路径。
   • 奖励 ($R_{fast}$)：二值奖励。如果提取的答案 $y_{fast}$ 等于真值 $y^{\ast }$，则奖励为 1，否则为 0。
2. 第二步：验证 (Verification)
   • 任务： 评估第一步的答案是否正确，输出“Yes”或“No”。
   • 限制： 短 Token 预算（如 2000 tokens）。
   • 动机： 训练模型的评估能力。验证通常比生成更容易，如果能自信地验证，就能节省后续计算资源。
   • 奖励 ($R_{verify}$)：基于验证正确性的加权二值奖励。为了防止模型因样本不平衡而总是输出 Yes 或 No，奖励权重根据当前 batch 的快思考准确率 ($p_{fast-acc}$) 动态调整。
3. 第三步：慢思考 (Slow Thinking - System 2)
   • 触发条件：
     • 训练时： 如果第一步答案错误，进入此步。
     • 推理时： 如果第二步验证输出“No”，进入此步。
   • 任务： 告知模型初始答案错误，要求其利用更长的 Token 预算（如 6000 tokens）进行深思熟虑、回溯和修正，给出新答案。
   • 动机： 训练模型的推理和修正能力。
   • 奖励 ($R_{slow}$)：二值奖励。如果新答案 $y_{slow}$ 正确，奖励为 1。
4. 第四步：总结 (Summarization)
   • 触发条件： 仅在训练模式下，且当慢思考得出了正确答案时触发。
   • 任务： 要求模型重新面对原始问题，将慢思考中冗长的正确路径总结为简洁的步骤。
   • 动机： 蒸馏与整合。将成功的 System 2 推理路径压缩回 System 1 的格式，以此来提升模型未来的“快思考”能力（即直觉）。
   • 奖励 ($R_{summary}$)：包含两部分：
     1. 正确性： 总结后的答案必须正确。
     2. 一致性： 引入一个 KL 散度相关的项（$\log P(a_{summary}|x_{fast})$），鼓励生成的总结在“快思考”的提示词下具有高概率。这强迫模型学习如何像“快思考”那样简洁地输出正确逻辑。

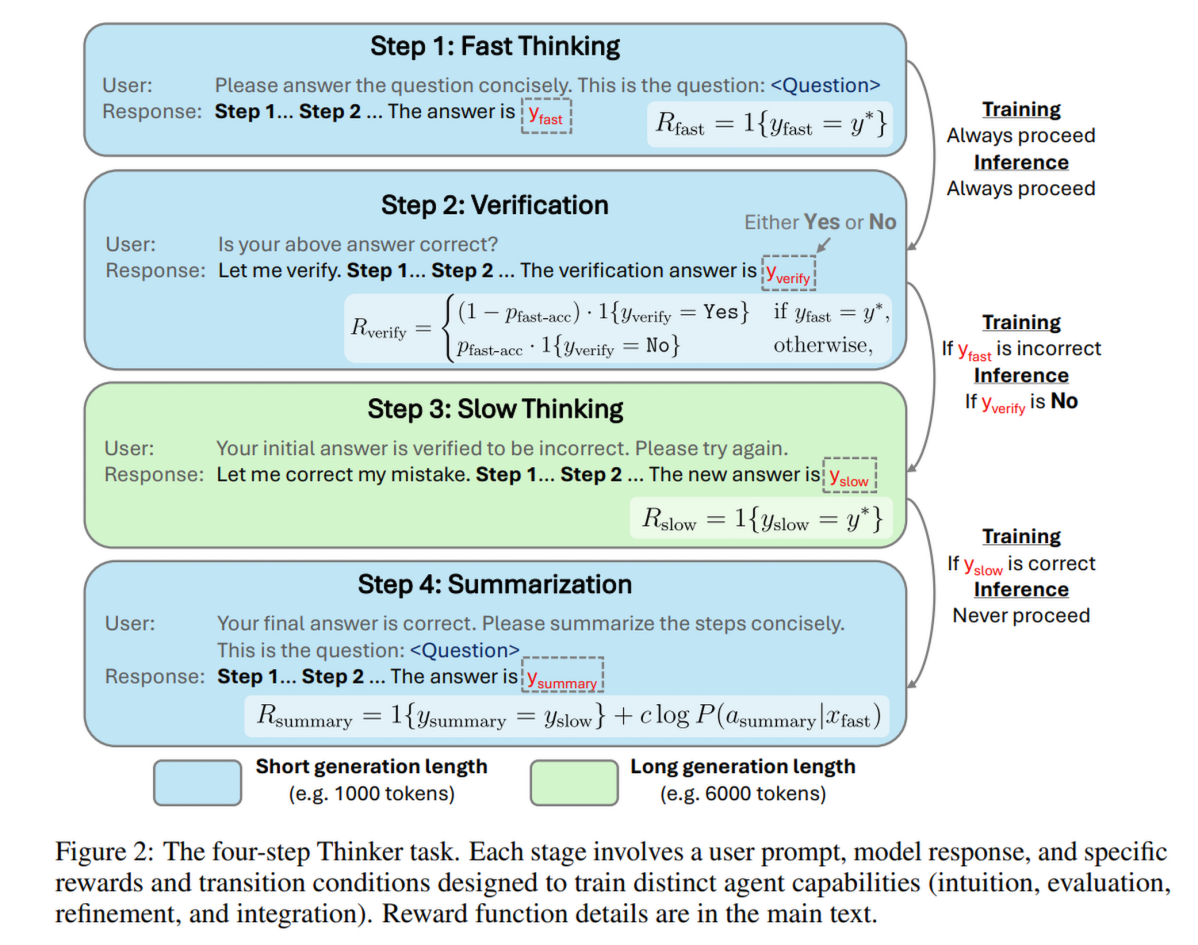
奖励函数如下：

$$\begin{array}{rl}{R}_{\text{fast}}& =1\{y_{\text{fast}}=y^{\ast }\}\\ R_{\text{verify}}& =\{\begin{array}{ll}(1-p_{\text{fast-acc}})\cdot 1\{y_{\text{verify}}=\text{Yes}\}& \text{if }{y}_{\text{fast}}=y^{\ast },\\ p_{\text{fast-acc}}\cdot 1\{y_{\text{verify}}=\text{No}\}& \text{otherwise}\end{array}\\ R_{\text{slow}}& =1\{y_{\text{slow}}=y^{\ast }\}\\ R_{\text{summary}}& =1\{y_{\text{summary}}=y_{\text{slow}}\}+c\log (P(a_{\text{summary}}|x_{\text{fast}}))\end{array}$$

2.2 训练与推理的区别

• 训练策略： 采用 PPO 算法。关键点在于分步信用分配。每一步的奖励只归属于该步，不向后传播到前面的步骤（步间折扣因子 $\gamma =0$），但步骤内部的 Token 奖励正常计算。这解决了传统 RL“一荣俱荣”导致的低效学习问题。
• 推理流程：
  1. 进行快思考。
  2. 进行验证。
  3. 如果验证为“Yes”，直接输出快思考答案（高效）。
  4. 如果验证为“No”，进行慢思考并输出慢思考答案（高质）。
  5. （推理阶段不进行总结步骤）。

3. 实验设置与结果

3.1 实验设置

• 模型： Qwen2.5-1.5B (基础模型) 和 DeepSeek-R1-Distill-Qwen-1.5B (R1.5B，已有推理能力的模型)。后续附录还验证了 7B 模型。
• 基线： 标准 QA 任务的 RL 微调（Baseline）、Open-Reasoner-Zero (ORZ)、SimpleRL。
• 数据集： 129K 数学问答数据集（Open-Reasoner-Zero 提供）。
• 评测集： MATH500, AIME 2024/2025, GPQA Diamond, OlympiadBench 等。

3.2 核心表现

1. 准确率显著提升：
   • 对于 Qwen2.5-1.5B：Thinker 平均准确率从 25.62% 提升至 27.33%
   • 对于 R1.5B：Thinker 平均准确率从 45.90% 提升至 50.98%，相对提升 11.1%
   • Thinker-Fast 模式（仅快思考）的表现： 仅使用第一步的输出，R1.5B 达到了 41.05% 的准确率，远超预训练模型（35.31%），且仅消耗极少的 Token（<1000），证明了直觉能力的提升
2. 训练动态：
   • Baseline 的准确率很快进入平台期，而 Thinker 的准确率（无论是 Fast 还是 Final）在持续上升
   • Token 效率：
     • 对于 R1.5B 模型，Baseline 随着训练进行，回复变得越来越长（学会了啰嗦和伪反思）
     • Thinker 模型的总回复长度反而缩短了。这是因为随着“快思考”准确率的提升，模型更多地在第一步就解决了问题，跳过了昂贵的“慢思考”阶段
3. 消融研究：
   • 移除总结步骤 (No Summarization)： 导致“快思考”的准确率下降。这证实了总结步骤通过将慢思考的智慧“蒸馏”给快思考，有效地提升了模型的直觉。
   • 反思模式分析： Thinker 模型生成的文本中，表示自我怀疑的词汇（如 “wait”, “however”）更少，推理更加直接。

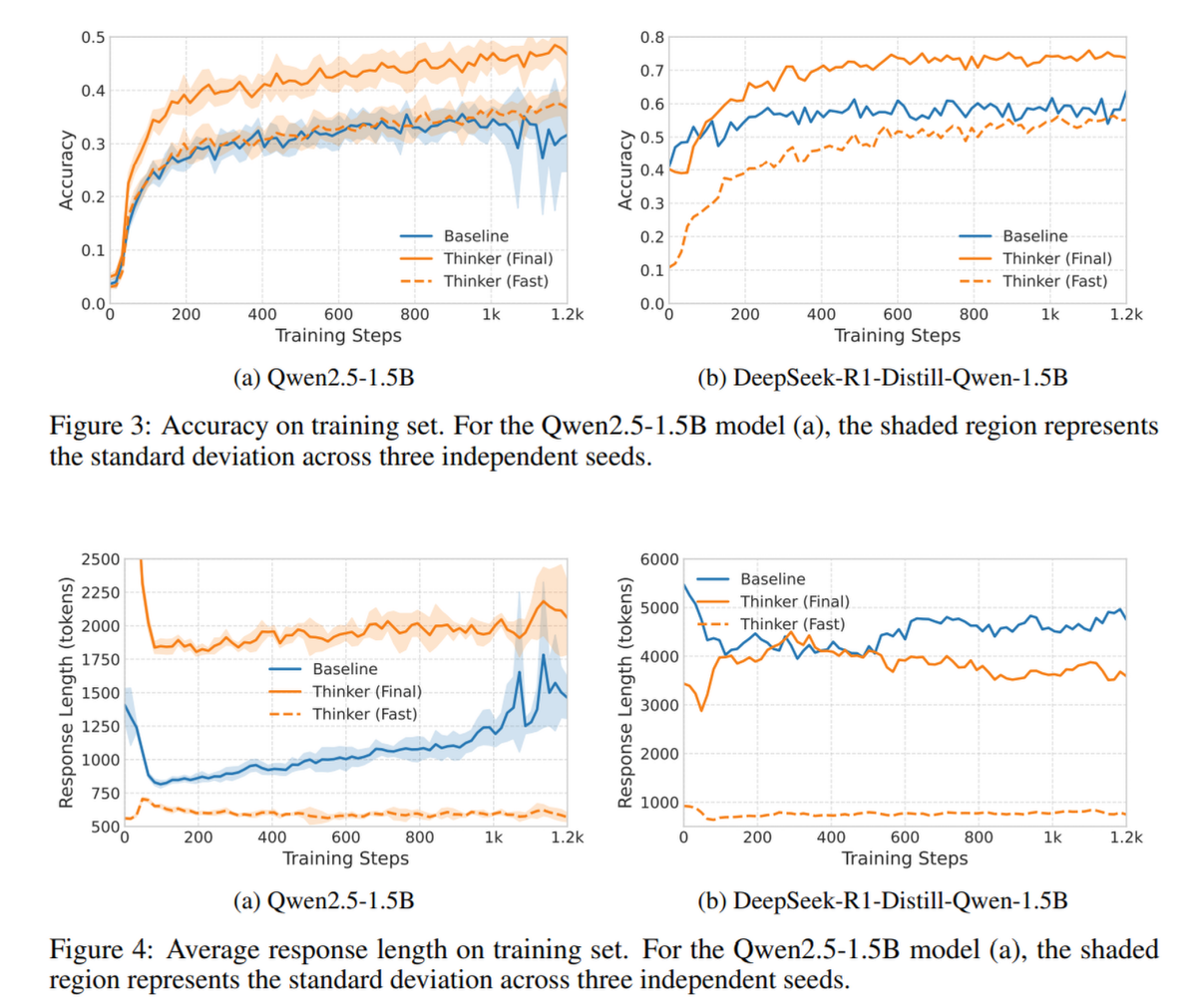
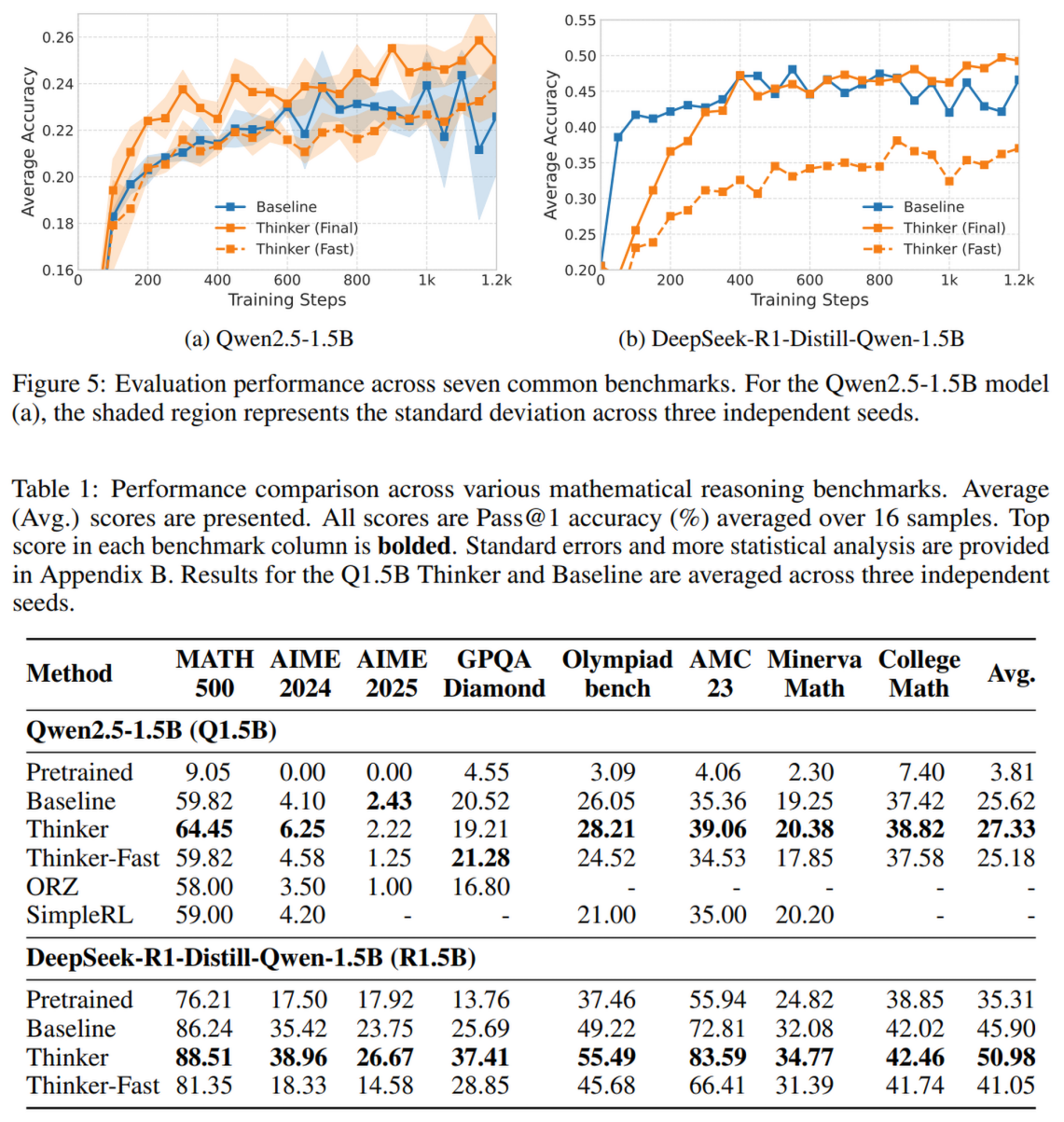
美中不足的是只对 1.5B 规模的模型进行了实验，说服力欠缺

4. 案例分析 (Case Study)

论文通过具体案例展示了 Thinker 的工作机制（附录 C）：

• 场景： 一个关于六边形路径的几何问题。
• Fast Thinking： 模型使用了一个错误的启发式直觉，算出了一个不可能的负数周长。
• Verification： 模型自我检查，发现初始假设（$S=a+4$）是错的，并推导出了正确关系。判定前一步错误。
• Slow Thinking： 利用验证阶段发现的正确关系，重新进行代数推导，得出了正确答案。
• Summarization： 将慢思考中复杂的纠错过程，整理成了一套清晰、逻辑连贯的解题步骤。

5. 论文结论与贡献

1. 解耦能力： 证明了直觉（快）和 慎思（慢）是两种互补且独特的能力，可以通过针对性的任务结构分别训练。
2. 高效推理： 相比于让模型自己在长 CoT 中漫无目的地搜索，Thinker 提供了一种结构化的框架，使得模型在简单问题上极其高效（Fast Mode），在困难问题上能有效修正（Slow Mode）。
3. 信用分配优化： 通过分阶段奖励，解决了 RL 在长推理链训练中奖励信号稀疏和含糊的问题。
4. 通用性： 该方法不依赖特定的 RL 算法（如 PPO）或模型架构，是一种通用的环境增强策略。

总结来说，Thinker 并没有发明新的 RL 算法，而是设计了一个更符合人类认知规律（快慢思考）的训练课程（Curriculum）/ 环境（Environment），成功地让小模型（1.5B）展现出了更强、更高效的推理能力。